如何计算固定长度模型的困惑度（PPL）

困惑度（PPL）是评估语言模型最常用的指标之一。在深入探讨之前，我们应该注意这个指标特别适用于传统语言模型（有时被称为自回归或因果语言模型），而对于像 BERT 这样的 masked language models 则没有明确定义（见模型总结）。

困惑度被定义为序列的指数化平均负对数似然。如果我们有一个标记化序列 $X = (x_0, x_1, \dots, x_t)$，那么 $X$ 的困惑度为，

$$
\text{PPL}(X) = \exp \left{ -\frac{1}{t}\sum*{i=1}^t \log p\theta (xi|x*{<i}) \right}
$$

其中 $\log p\theta (x_i|x{<i})$ 是第 i 个标记的对数似然，条件是根据我们的模型前面的标记 $x_{<i}$。直观上，它可以被认为是评估模型在语料库中指定标记集合上预测均匀性的能力。重要的是，这意味着标记化程序直接影响模型的困惑度，这在比较不同模型时应始终考虑。

这也相当于数据和模型预测之间的交叉熵的指数化。想要了解更多关于困惑度及其与每字符位数（BPC）和数据压缩的关系的直觉，可以查看这篇在 The Gradient 上的精彩博客文章。

Calculating PPL with fixed-length models

如果我们不受模型上下文大小的限制，我们会通过自回归地分解序列并在每一步都基于整个前序子序列来条件化，从而评估模型的困惑度，如下图所示。

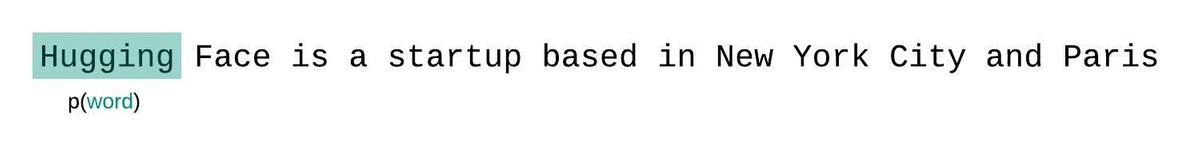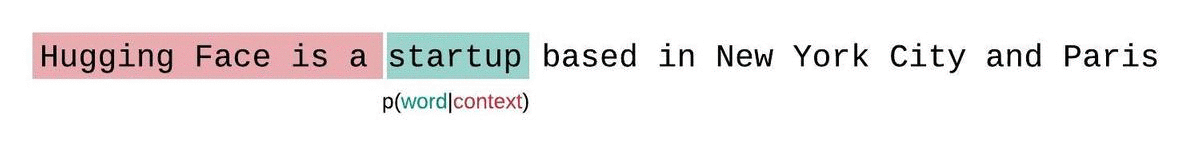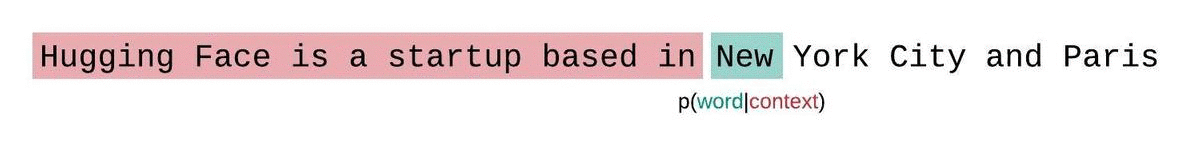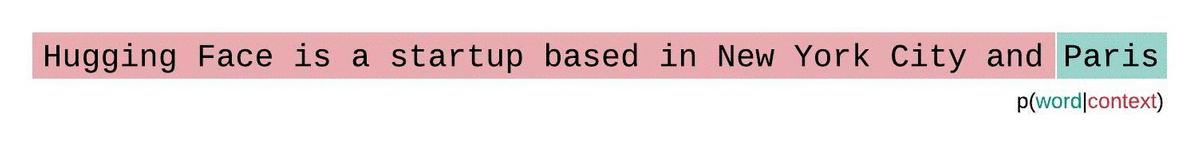
Full decomposition of a sequence with unlimited context length

然而，在处理近似模型时，我们通常受到模型可以处理的标记数量的限制。例如，GPT-2的最大版本有固定的 1024 个标记长度，所以当 $t$ 大于 1024 时，我们无法直接计算 $p\theta(x_t|x{<t})$。

相反，序列通常被分解成等于模型最大输入大小的子序列。如果模型的最大输入大小是 $k$，那么我们通过只条件化前 $k-1$ 个标记（而不是整个上下文）来近似计算一个标记 $x_t$ 的似然。在评估模型序列的困惑度时，一种诱人但次优的方法是将序列分解成不相交的块，并独立地累加每个段的分解对数似然。

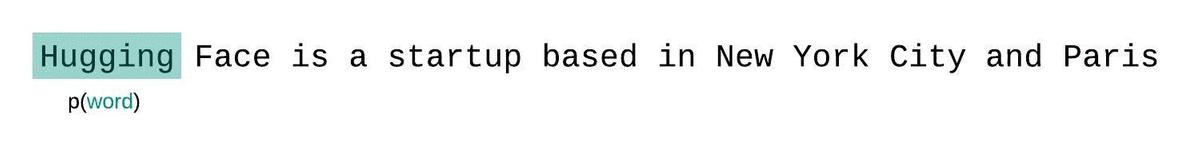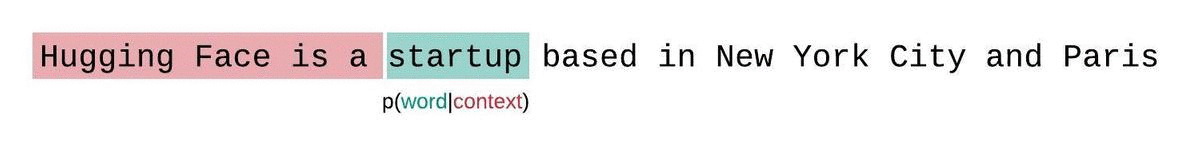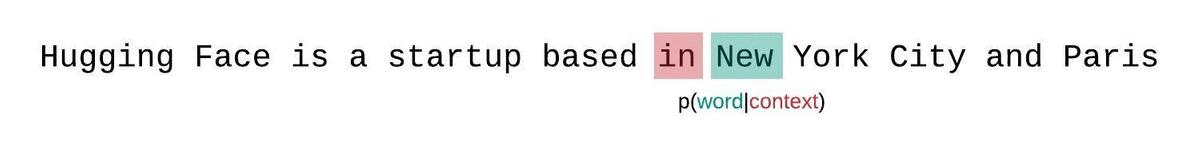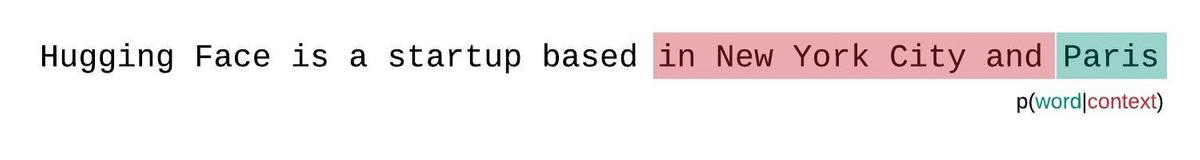
Suboptimal PPL not taking advantage of full available context

这种计算很快，因为每个段的困惑度可以在一次前向传递中计算出来，但这是一个较差的完全分解困惑度的近似，并且通常会产生更高（更差）的 PPL，因为模型在大多数预测步骤中的上下文较少。

相反，应该使用滑动窗口策略来评估固定长度模型的 PPL。这涉及到重复滑动上下文窗口，使模型在做出每个预测时拥有更多的上下文。

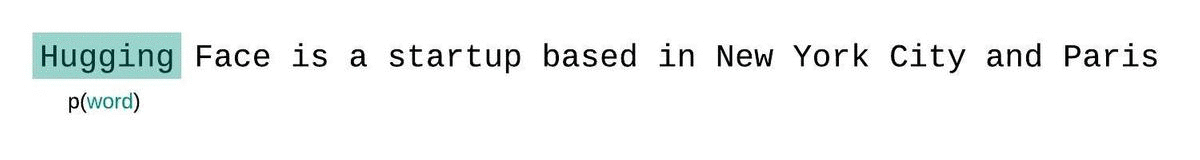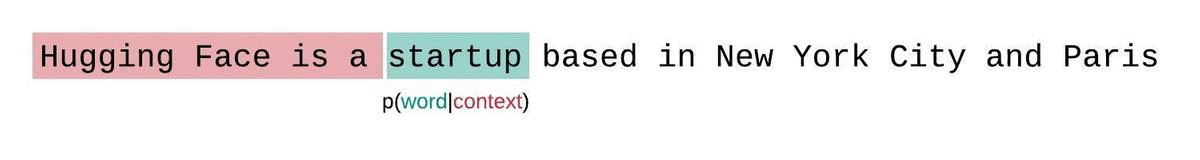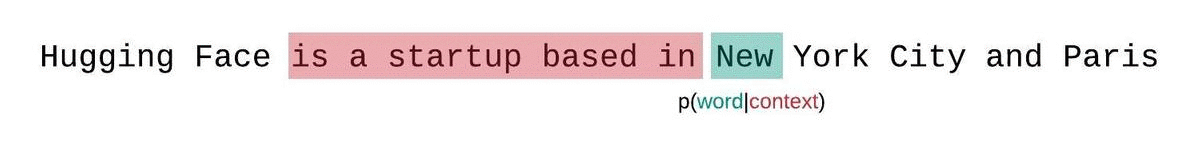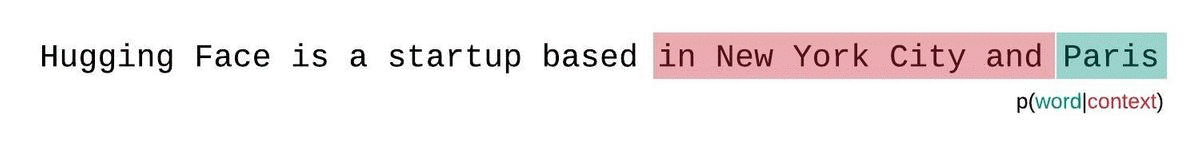
Sliding window PPL taking advantage of all available context

  1. 无限上下文分解： 如果没有对模型输入长度的限制，我们可以在每一步都使用整个前序子序列来预测下一个标记。这样可以最准确地评估模型的性能，因为每次预测都考虑了所有先前的信息。

  2. 固定长度限制： 实际中，大多数模型如 GPT-2 有固定的输入长度限制（例如 1024 个标记）。当序列长度超过这个限制时，不能直接计算每个标记的条件概率，因为不能将整个序列作为条件。

  3. 分块近似： 一种处理长序列的方法是将序列分解成多个与模型最大输入长度相等的子序列。每个子序列单独评估，但这种方法可能会因为没有使用完整的上下文而导致更高的困惑度。

  4. 滑动窗口策略： 为了更好地利用可用的上下文，可以使用滑动窗口策略。这种方法通过不断移动上下文窗口来尝试在每次预测时为模型提供更多的上下文信息，从而更接近于使用完整上下文的理想情况。

  5. 跨步滑动窗口： 一个实际的折中方法是使用跨步滑动窗口，这样可以在保证一定效率的同时，为每次模型预测提供足够的上下文，从而改善困惑度的计算和模型预测的准确性。

这些方法都是为了解决因模型输入长度限制而不能直接评估整个序列的问题，试图通过不同的技术使评估更加准确，同时考虑到计算资源的有效使用。